https://jasmine46.tistory.com/81
[강화학습][1] Reinforcement Learning
Reinforcement Learning 원하는 작업의 달성을 위한 별도의 구체적인 지정없이 보상(Reward)과 벌칙 (Punishment)를 통한 Agent 학습 목표 : 축적된 보상을 최대화하는 control policy를 찾는 것 St : t시간의 St..
jasmine46.tistory.com
Bellman Equation (벨만 방정식)
어떤 상태 (state)에서 value를 구할 때, 벨만 방정식을 이용합니다.
이 때 다이나믹 프로그래밍 (Dynamic Programming)을 이용하여 작은 문제로 나누고 Iteration하는 방법으로 문제를 해결합니다. 기대방정식과 최적방정식으로 나누어 살펴보겠습니다.
1) 벨만 기대방적식 (Bellman Expectation Equation)
Policy $\pi$를 알 때 사용합니다. policy라는 것은 Agent 입장에서 어떤 액션을 할 확률이라고 생각하면 됩니다.
π(a∣s)=P[At=a∣St=s] → State = s일때, action a를 할 확률입니다.
$V_{\pi}(s)$ 는 state가 주어질때 value를 파악하고자 할때 사용합니다.
특정 state에서의 Value는 총 보상의 합입니다.
① State / Action에 대한 Value
$V_{\pi}(s) $ = $ E_{\pi}$$[ Return_t | S_t = s ] $
▶ $ Return = R_{t+1} + γ*R_{t+2} + γ^2*R_{t+3} + .. $
▶ $V_{\pi} = E_{\pi} [r_{t+1} + γ * V_{\pi}(S_{t+1})]$
$Q_{\pi}(s, a) $ = $ E_{\pi}$$[Return_t | S_t = s, At = a ] $
▶ $Q_{\pi}(s, a) $ = $ E_{\pi}$$[r_{t+1} + γ * Q_{\pi}(S_{t+1}, A_{t+1}) | S_t = s, At = a ] $
[강화학습][1]에서 정리했던 수식을 그대로 사용하였습니다.
② State / Action에 대한 Value를 다른 방식으로 변경
$V_{\pi}(s)$ = ${\Sigma}$ ${\pi}$( a ∣ s ) * $Q_{\pi}(s, a)$
▶ State의 Value = Agent가 특정 Action을 할 확률 * 액션에 대한 value
$Q_{\pi}(s, a)$ = $r^a_t$ + ${\gamma}$*${\Sigma}$$P^a_{ss'}$*$V_{\pi}(s')$
▶ 액션의 Value = 액션에 대한 reward + sum(액션을 했을 때 다른 state'로 이동할 확률 * state'의 value)
③ ②의 수식을 대입
$V_{\pi}(s)$ = ${\Sigma}$ ${\pi}$( a ∣ s ) * $Q_{\pi}(s, a)$
$Q_{\pi}(s, a)$ = $r^a_t$ + ${\gamma}$*${\Sigma}$$P^a_{ss'}$*$V_{\pi}(s')$
▶ $V_{\pi}(s)$ = ${\Sigma}$ ${\pi}$( a ∣ s ) ${\bigg(}$ $r^a_t$ + ${\gamma}$*${\Sigma}$$P^a_{ss'}$*$V_{\pi}(s')$ ${\bigg)}$
마찬가지로, Action은 하기와 같이 표현됩니다.
$Q_{\pi}(s, a)$ = $r^a_t$ + ${\gamma}$*${\Sigma}$$P^a_{ss'}$*$V_{\pi}(s')$
▶ $r^a_t$ + ${\gamma}$${\Sigma}$$P^a_{ss'}$ ${\Sigma}$ ${\pi}$( a' ∣ s' ) * $Q_{\pi}(s', a')$
2) 벨만 최적방정식 (Bellman Optimality Equation)
벨만 최적방정식은 모든 Agent의 Action 중에서 최적을 찾는다 라고 이해를 하면 직관적일 것 같습니다.
어떤 State에서의 최적 Value ($V_*(s)$)는 $Max_π V_{\pi}(s)$ 입니다.
마찬가지로, 액션의 최적 Value $Q_*(s, a)$ = $Max_{\pi}$ $Q_{\pi}(s, a)$입니다.
① State / Action에 대한 최적 Value
$V_*(S_t)$=$Max_a$ $E[r_{t+1} + {\gamma}V_*(S_{t+1})]$
$Q_*(S_t, A)$ = $E[r_{t+1} + {\gamma}Max_aQ_*(S_{t+1}, a')$
② 최적의 State Value는 Action들의 Value 중 Max값을 지니는 Value
$V_*(S)$= $Max_a Q_*(S, a)$
최적의 Action Value는 기대방정식의 Q(s, a)와 동일합니다.
$Q_*(s, a)$ = $r^a_s$ + ${\Sigma}$$P^a_{ss'}V_*(S')$
③ 기대방정식과 동일하게 대입합니다.
$V_*(S)$= $Max_a$$Q_*(S, a)$
→ $V_*(S)$= $Max_a$ ${\bigg(}$ $r^a_s$ + ${\Sigma}$ $P^a_{ss'}V_*(S')$ ${\bigg)}$
$Q_*(s, a)$ = $r^a_s$ + ${\Sigma}$$P^a_{ss'}$ $V_*(S')$
→ $Q_*(s, a)$ = $r^a_s$ + ${\Sigma}$$P^a_{ss'}$ $Max_a Q_*(S', a')$
3) Basic Code (Grid World)
# 초기 1회 실행
!pip install gym==0.20
!pip install pygame
!pip install gridworld
# Import dependencies
import numpy as np
import sys
from gridworld import GridworldEnv as Grid
import numpy as np
env = Grid()
# State : 4x4 Matrix 총 16개 (S0~S15), Action : 총 4개 (상/하/좌/우)
print("# state:", env.nS, "# action:", env.nA, end='\n')
env.reset() # env (환경 초기화)
# _render() => envioronment를 visulalize 해준다.
env._render()
# 0: Up, 1: Right, 2: Down, 3: Left
# step(2) => down 동작을 한 것 입니다.
env.step(2)
print()
env._render()
각 State에 대한 Value를 반복 평가를 하게되면, 어느 순간에 수렴을 하게 됩니다.
하지만, 중요한 것은 각 State에 대한 Value를 평가를 하는 것이 아닌
최적의 정책을 찾아내는 것입니다.
우선, 각 Value를 평가를 하겠습니다.
앞에서 구해보았던 벨만 기대방정식을 이용하여 각 State에 대한 Value를 반복적으로 평가하면 됩니다.
$V_{\pi}(s)$ = ${\Sigma}$ ${\pi}$( a ∣ s ) ${\bigg(}$ $r^a_t$ + ${\gamma}$*${\Sigma}$$P^a_{ss'}$*$V_{\pi}(s')$ ${\bigg)}$
class Grid_Model_Basic(object):
def __init__(self, pi_policy, env):
self.pi_policy = pi_policy
self.env = env
self.discount_factor = 1.0
def value_eval_repeat(self, n):
# init value = s0~s15 = 0으로 초기화
v = np.zeros(env.nS) # (16, )
# n 회 repeat
for _ in range(n):
v_next = np.zeros(env.nS) # next state value
# s0~s15까지 value update
for s in range(env.nS):
for action, policy_prob in enumerate(self.pi_policy[s]):
for transition_prob, next_state, reward, _ in env.P[s][action]:
# value update
v_next[s] += policy_prob*(reward + self.discount_factor \
* transition_prob * v[next_state])
v = v_next
return np.round(v.reshape(4, 4), 2)
pi_policy = np.array([0.25]*64).reshape(16, 4)
value = Grid_Model_Basic(pi_policy, env)
value.value_eval_repeat(1) # 반복 횟수 지정
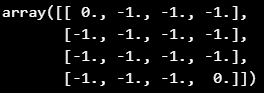
for n in [1, 2, 3, 10, 50, 100, 200, 300]:
print("N회 반복 평가 : {}".format(n))
print(value.value_eval_repeat(n), end='\n\n')


평가 결과, 100회 이상부터는 크게 변화가 없으며 각 State의 Value가 어느 특정한 값으로 수렴이 된다는 것을 확인할 수 있습니다.
'스터디 공간' 카테고리의 다른 글
| [Python-Leetcode] 6. Zigzag Conversion (difficulty : Medium- ☆☆) (0) | 2022.05.09 |
|---|---|
| [Python-Leetcode] 509. Fibonacci Number (difficulty : Easy - ☆) (0) | 2022.05.06 |
| [강화학습][1] Reinforcement Learning (0) | 2022.05.05 |
| [Python-Leetcode] 13. Roman to Integer (difficulty : Easy - ☆) (0) | 2022.05.05 |
| [Python-Leetcode] 1. Two Sum (difficulty : Easy - ☆) (0) | 2022.05.01 |




댓글