반응형
[Python Data Science] 베르누이, 이항분포
1. 베르누이 분포
- 매번 실험의 결과 -> 성공 / 실패 둘장 하나입니다.
- 동전을 던져, 앞 혹은 뒤가 나올 때의 확률 분포를 베르누이 분포라고 볼 수 있습니다.
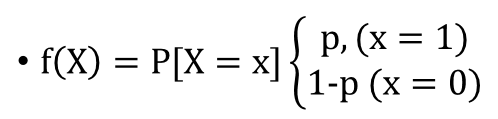
- 동전을 예로 들면, 앞이 나올 확률 0.5 / 뒤가 나올 확률 0.5 입니다.
- P(X=’앞’) = 0.5, P(X=’뒤’) = 0.5 라고 표현할 수 있습니다.
2. 이항 분포
- 매 시행마다, 결과가 성공 혹은 실패라면 N번 반복했을 때의 성공횟수를 이항분포 라고 볼 수 있습니다.
- 성공확률 p와 시행횟수 N에 대해서, 하기와 같이 표현이 가능합니다.
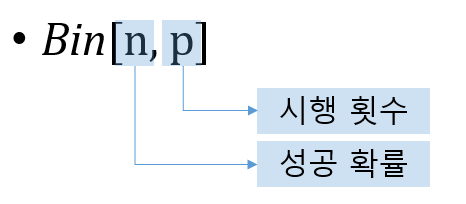
- 이항분포의 확률은 하기와 같습니다.
- 베르누이 분포를 N번 반복한 것으로 nCm이 앞에 붙습니다.

- 기대값, 분산 ▶
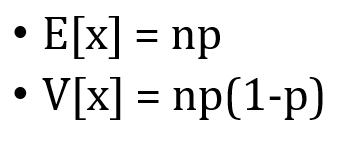
- 치료율이 0.5인 치료법이 있다고 가정
- 10명에게 독립적으로 치료를 적용
- 이때 기대값은 E[x] = np = 10*0.5 = 5 / V[x] = np(1-p) = 10(0.5)(0.5) = 2.5인 것을 위의 식을 통해서 구할 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
p = 0.5 # 성공확률
n = 10 # 총 10번 시행
#앞의 이항분포 확률수식
def get_pmf(n, m, p):
return comb(n, m)*(p**m)*((1-p)**(n-m))
result = []
for m in range(1, n+1):
# 시행횟수, 1~10번까지의 확률 분포 확인
result.append(get_pmf(n, m, p))
#막대 그래프로 plot
plt.bar(range(1, n+1), result)
- 막대그래프를 살펴보면, 성공률이 0.5이므로 10명 중 5명이 치료되었을 때가 가장 높다는 것을 알 수 있습니다.
- 평균(기대값)을 중심으로 정규분포와 비슷한 종 모양이 생깁니다.
3. 포아송 분포
- 단위시간 / 공간에서 어떤 사건이 발생하는 횟수에 따른 확률이며, X ~ POI[λ] 로 표현이 가능합니다.
- 예) 하루 동안의 발생되는 교통사고의 건수가 100건이라면 POI[100]으로 표현할 수 있습니다.
- 포아송 분포는 기댓값과 분산이 서로 같습니다.
- ▶
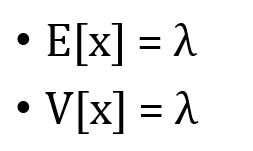
- 포아송 분포의 확률 질량 함수 (POI[λ])

Q. 어떤 책의 10페이지를 검사하였을 때 나온 오타의 수가 20개 입니다.
이때, 한 페이지를 검사하였을 때 5개의 오타가 나올 확률은?
A. 10 Page에서 나온 오타가 20개 이므로 1페이지의 평균은 2입니다. → λ = 2
POI[2] = 3.6%
4. 지수분포
- 포아송 확률을 따르는 사건이 1번 발생되고, 다음에 발생하기까지 걸리는 시간을 확률 변수로 둘때의 확률입니다.
- 야구 1이닝 동안 평균적으로 3번 실책을 할 때 → 횟수 (포아송 분포)
- 1번 실책을하고 다음 번 실책을 할때까지의 시간 → 시간 (지수 분포)
- EXP[λ]로 표기합니다.
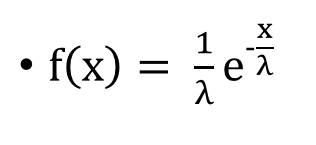
- 포아송분포의 λ(평균횟수)와 역수의 관계를 보입니다.
- 1시간 동안 교통사고가 5번 발생할 때, → 교통사고가 발생하는 시간은 1/5 인 약 12분으로 역수 라는 것을 알 수 있습니다.
- 포아송 분포의 기댓값이 커질 수록, 단위시간동안 발생횟수가 커진다는 것을 의미하므로 사건 발생 시간은 짧아진다고 볼 수 있습니다.
반응형
'스터디 공간' 카테고리의 다른 글
| [Programmers] 해시 - 전화번호 목록 (0) | 2021.08.08 |
|---|---|
| [Programmers] 해시 - 완주하지 못한 선수 (0) | 2021.08.08 |
| [Python Data Science] 확률/통계 기초 알아보기 (0) | 2021.08.07 |
| [프로그래머스 - SQL 기초 문제 스터디] 중성화 여부 파악하기 (STRING) (1) | 2021.04.11 |
| [프로그래머스 - SQL 기초 문제 스터디] 이름에 el이 들어가는 동물 찾기 (STRING) (0) | 2021.04.11 |




댓글